
This is an old revision of the document!
The objective of this lab activity is to investigate the characteristics of the Peltz oscillator configuration.
Unlike the Clapp, Colpitts and Hartley oscillators which have a single transistor, the Peltz configuration uses two transistors. Looking at figure 1, we see that transistor Q1 is configured as a common base amplifier stage. The resonate tank consisting of L1 and C1 provides the collector load. Its output at the collector feeds the base of transistor Q2 which is configured as an emitter follower (common collector) stage. The positive feedback which is required for oscillation is formed when the output of the emitter follower ( emitter Q2 ) is connected back to the input of the common base stage at the emitter of Q1. The voltage gain of the common base amplifier stage is a maximum at the parallel resonate frequency of the LC tank where its impedance approaches infinty. The gain of the emitter follower is always slightly less than one. The combined gain around the loop will be much greater than 1 at resonance to sustaine oscillation.
Figure 1 Basic Peltz Oscillator configuration
The resonate frequency of the LC tank is given by:
The peak to peak swing across the LC tank is limited in this oscillator configuration. As the voltage on the base of Q2 swings more positive than ground, the collector of Q2, the collector base junction will forward bias limiting the maximum positive swing to around one forward diode drop. Similarly, for the peak negative swing, when the collector of Q1 swings negative enough to forward bias the collector base junction of Q1. When the collector base junction of a BJT transistor is forward biased the base current increases dramatically. We can make use of this increased base current to increase the peak to peak swing seen across the LC tank. If we insert resistors in series with the base of both Q1 and Q2, as shown in figure 2, the additional current through the resistors will lower the base voltage of Q1 and Q2 at the extremes of the LC tank voltage.
Figure 2 Increased output swing
Build a simulation schematic of the Peltz oscillator as shown in figures 1 and 2. Calculate a value for bias resistor R1 such the collector current in transistors Q1 and Q2 is greater than 200 uA each. Assume the circuit is powered from a -5V power supply. Calculate a values for C1 and L1 such that the resonate frequency will be at least 1 MHz. Perform a transient simulation. The peak to peak output swing across the LC tank should be limited to less than +/- 1 forward diode drop ( ~ +/-0.6 V ). Calculate and simulate values for R2 = R3 such that the output swing increases to at least +/- 1.25V. Save these results to compare with the measurements you take on the actual circuit and to include with your lab report.
ADALM2000 Active Learning Module
Solder-less breadboard
Jumper wires
2 - small signal NPN transistor (2N3904)
1 - 10 KΩ resistor
2 - 4.7 KΩ resistors
1 - 100 uH inductor
1 - 100 pF capacitor
Build the Peltz oscillator circuit shown in figure 3 on your solder-less breadboard. The green squares indicate where to connect the ADALM2000 module scope channels and power supply. Be sure to only turn on the power supply after you double check your wiring.
Figure 3 Peltz oscillator circuit
Set both scope inputs to 200 mV/div and the time base to 1 uSec/div. Set the trigger on the rising edge of channel 1.
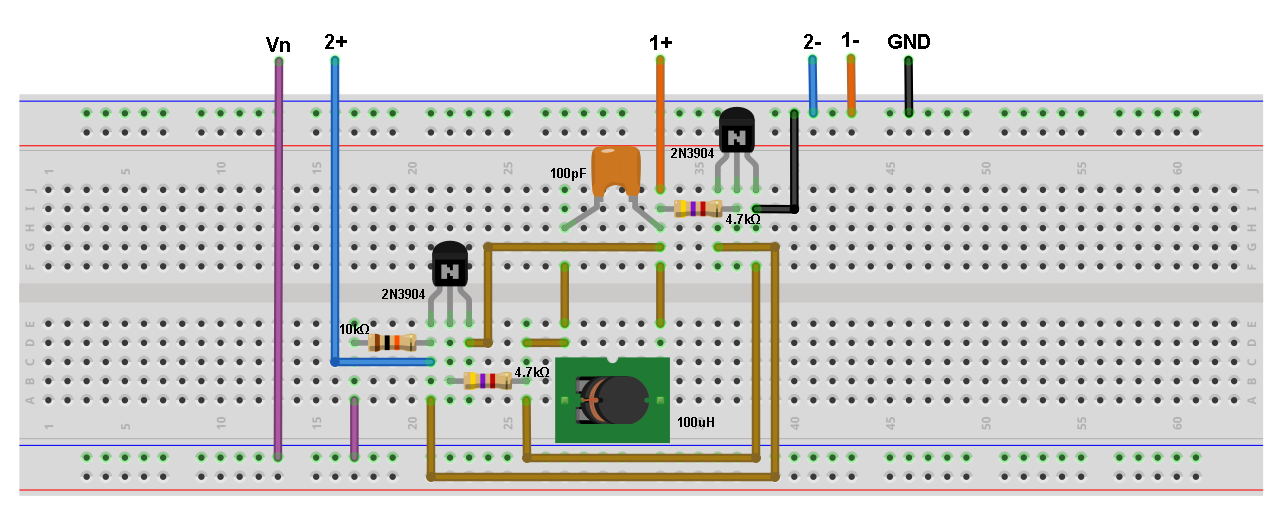
Figure 4 Peltz oscillator circuit breadboard connections
Turn on the -5V power supply. Observe the output waveform across the LC tank on scope channel 1. You can also observe the waveform seen at the emitters of Q1 and Q2 using scope channel 2.

Figure 5 Peltz oscillator circuit Scopy shot
Notice that the output signal swings positive and negative around ground (0 V). Measure the frequency of the output waveform. Measure the peak to peak amplitude R2 and R3 replaced with shorts (i.e. 0 Ω). Compare this to the peak to peak amplitude you measure with R2 and R3 in the circuit. Try other values for R2 and R3. Is there a practical upper limit to the values of R2 and R3 and the peak to peak amplitude? Does changing the value of R2 and R3 effect the oscillating frequency? If so why?
Compare the shape of the output waveform with R2 and R3 as shorts vs with them set to various values. How does the shape change and why?
Resources:
How does the measured output sinewave frequency compare to what you calculate using the formula for an LC tank and the values for L and C you used?
For Further Reading:
Return to Lab Activity Table of Contents.