 This version (06 Aug 2017 12:37) is a draft.
This version (06 Aug 2017 12:37) is a draft.
This is an old revision of the document!
Basic ideas behind the classic current mirror are revealed below by using the building approach proposed in the Wikibooks story How to Reverse Current Direction.
A current mirror is a circuit block which functions to produce a copy of the current in one active device by replicating the current in a second active device. An important feature of the current mirror is that it has a relatively high output resistance which helps to keep the output current constant, regardless of load conditions. Another feature of the current mirror is that it has a relatively low input resistance which helps to keep the input current constant, regardless of drive conditions. The current being 'copied' can be, and often is, a varying signal current. Conceptually, an ideal current mirror is simply an ideal current amplifier with a gain of -1. The current mirror is often used to provide bias currents and active loads in amplifier stages. Given a current source as the input, we convert the current (entering the current mirror) into a voltage and then use this voltage to control a current sink (the current exiting the mirror); as a result, we obtain a current sink (figure 11.1a). Conversely, given a current sink as the input, we convert the input current (exiting the current mirror) into a voltage and then use this voltage to control a current source (figure 11.1b); as a result, now we obtain a current source. We can generalize this basic current mirror structure in a first conclusion:
A current mirror consists of a current-to-voltage converter consecutively connected to a voltage-to-current converter.
Figure 11.1, Current Mirror (a) Sink (b) Source
It should be noted that the two converters may have a linear relationship (for example where VOUT = IINR and IOUT= VIN/R) like a resistor, but this linear relationship is not required. The converters might be non-linear devices having whatever transfer or I to V characteristics that may even depend on another quantity (such as temperature); the only requirement is the characteristics be the inverse of each other. For example, if the I to V converter implements a function v = f(i) and the other represents the inverse function i = f -1(v) the whole function is v = f(i) = f(f -1(v)) . So, we can formulate the second conclusion: a current mirror consists of two consecutively connected converters that have inverse transfer functions.
We need a configuration where our active element of choice, a transistor, serves as the desired current-to-voltage converter. However, the transistor is a unidirectional device, where for the BJT the base emitter voltage controls the collector current or for the FET the gate source voltage controls the drain current. Producing the opposite where the collector current controls the VBE is not possible in the conventional use of the device as a common emitter amplifier. The solution is to incorporate negative feedback. In this case that means making the transistor adjust its base emitter or gate source voltage, VBE or VGS, so that the collector or drain current is IIN = (V1-VBE)/R. For this purpose, we simply connect the collector to the base or gate to drain. This results in 100% parallel negative feedback (figure 11.2). As a result, with this reversed transistor, the collector current serves as the input quantity while the base-emitter voltage VBE serves as the output quantity with a logarithmic transfer function. The input part of the simple BJT current mirror is just a bipolar transistor with 100% parallel negative feedback. Similarly, a diode connected enhancement mode MOS FET (gate tied to drain) will serve as a similar current to voltage converter with VGS as the output quantity rather than VBE.
Figure 11.2, Current to Voltage Converter
A bipolar transistor can be driven by a voltage or by a current. If we consider the base emitter voltage, VBE, as the input and the collector current, IC, as the output (figure 11.3), we can think of a transistor as a non-linear voltage-to-current converter having an exponential characteristic. The base can be directly driven by the voltage output of the I-to-V converter we just discussed. The collector provides the output terminal of our simple current mirror: The output V to I converter stage of the simple current mirror is just a transistor acting as a non-linear (exponential for BJT) voltage-to-current converter. Again if a MOS transistor were used for the input stage the output stage would be a MOS transistor with the gate serving as the voltage input and the drain as the current output.
Figure 11.3, Voltage to Current Converter
The final step is to connect the output of the input stage (the base emitter junction of Q1) to the input of the output stage (the base emitter junction of Q2) to build the basic BJT current mirror circuit (figure 11.4). At this point we will concentrate on the issues involved with the BJT current mirror and pick back up with the MOS current mirror in section 11.6.
Figure 11.4, BJT Current Mirror
If transistors Q1 and Q2 in figure 11.4 are identical (that is have the same size emitter and thus equal IS) the input current to output current ratio or gain is ideally 1. There are often occasions when a gain other than one is required. When building circuits from discreet devices only simple integer ratios are possible while in microelectronic integrated circuits it is possible to make transistors with arbitrary emitter areas, A. However, even in integrated circuits the best design practice is to use identical unit size transistors when making current mirrors.
Figure 11.4.1, Current Mirror with non-unary gain ratio
If on the input side of the mirror we connect N identical devices in parallel and connect M devices in parallel on the output side, the gain of the mirror will be M/N. In figure 11.4.1 we see an example where 2 (N=2) devices are connected together on the input and 3 (M=3) devices are connected together on the output. The mirror gain will thus be 3/2 or 1.5. Since all five transistors share the same VBEvoltage, their collector currents, IC, will all be equal. The input current IIN splits equally in Q1 and Q2 such that:
,
or
There are three primary error sources that make the simple 2 transistor mirror less than ideal. The first is the mirror gain. Ideally IOUT should exactly equal IIN. There are systematic and random factors that make this not the case. The second is the incremental output resistance, which determines how much the output current varies with the voltage seen at the mirror output. The third limitation is the minimum voltage drop across the output leg of the mirror necessary to maintain the desired output current. This minimum voltage, called output compliance, is determined by the need to keep the output transistor of the mirror in the active region. There are also a number of secondary performance issues with mirrors, for example, temperature stability and frequency response.
An error source in this simple BJT based current mirror is that the transistors Q1 and Q2 (figure 11.4) each remove a base current IB from the input current IIN. As a result, the output current is smaller than the input current:
As was already discussed, current mirrors can just as easily be made from MOS FET transistors. The I-to-V and V-to-I functions are different but of course are still the inverse of each other. A significant advantage of the MOS current mirror is the lack of base current induced error that BJT current mirrors suffer. There are methods to correct or compensate for the base current in BJT current mirrors which will be discussed in detail in later sections of this chapter.
It is necessary to keep the output (BJT) transistor out of saturation, VCB = 0 V. Or from another perspective, not allow the collector base junction to forward bias. That means the lowest output voltage that results in the correct output current, the compliance voltage, is VOUT = VCV = VBE under bias conditions with the output transistor at the output current level IC and with VCB = 0 V or, restating the VBErelation from earlier:
Where VT is the thermal voltage and IS is the reverse saturation current.
The VCB of Q1 in the mirror is zero. If VCB is greater than zero in the output transistor Q2, the collector current in Q2 will be somewhat larger than Q1 due to the Early effect. In other words, the mirror has a finite output resistance given by the rO of the output transistor, namely:
Where:
VA is the Early voltage
VCB is the collector-to-base voltage
As we learned in an earlier chapter, the inclusion of emitter degeneration resistors (RE1 and RE2 in figure 11.5) can increase the effective collector impedance seen at the mirror output. In order for the mirror gain to remain equal to 1, RE1 must of course equal RE2. The added voltage drop across the emitter resistor RE2 (IOUT x RE2) adds to the minimum allowable output voltage (see section 11.5.2).
While resistors could also be added to the sources in an MOS based mirror, it is often more effective to simple increase the channel length, L, of the transistors. The longer the channel the less it is affected by the channel length modulation due to the increasing drain voltage.
Figure 11.5, Emitter degeneration included to boot output resistance.
It is important to note that the inclusion of emitter resistors does not reduce the reduction in the output current IOUT caused by the finite beta of Q1 and Q2. A compensating voltage can be inserted by including resistor RB, of the correct value, as shown in figure 11.6.
Figure 11.6, Adding a resistor in the base of Q1 tends to compensate for the finite beta of Q2
For VCB close to zero (that is, neglecting base-width modulation errors) the necessary value for RB is:
For example, using A = 2 ( a mirror gain of 2 ), IIN = 1mA, so rE = 26Ω and RE1 = 500Ω (introducing about 500mV of degeneration) RB should be 1578Ω if β is enough larger than A so that factor can be ignored, or 1626Ω if it is included and beta is 100. Clearly, this compensation method becomes unpredictable when β is small and is comparable to A and will never be precise because β1 and β2 are not in general equal. However, this technique can be of practical utility in many cases.
The simple current mirror can, obviously, also be implemented using MOSFET transistors, as shown in figure 11.7. We know that transistor M1 is operating in the saturation region because VDS is greater than or equal to VGS. Transistor M2will also be in saturation so long as the output voltage is larger than its saturation voltage. In this simple configuration, the output current IOUT is directly related to IIN.
Figure 11.7 Simple MOS current mirror
The drain current of a MOSFET ID is a function of both the gate to source voltage and the drain to gate voltage of the MOSFET given by ID = f (VGS, VDG), a relationship derived from the functionality of the MOSFET device. In the case of transistor M1 of the mirror, ID = IIN. Input current IIN is a known current, and can be provided by a resistor as shown in the figure, or by a threshold-referenced or self-biased current source to ensure that it is constant, independent of voltage supply variations.
Using VDG=0 for transistor M1, the drain current in M1 is ID = f (VGS,VDG=0), so we find: f (VGS, 0) = IIN, implicitly determining the value of VGS. Thus IIN sets the value of VGS. The circuit in the diagram forces the same VGS to apply to transistor M2. If M2 also is biased with zero VDG and provided transistors M1 and M2 have good matching of their properties, such as channel length, width, threshold voltage etc., the relationship IOUT = f (VGS,VDG=0 ) applies, thus setting IOUT = IIN; that is, the output current is the same as the input current when VDG=0 for the output transistor, and both transistors are matched.
The drain-to-source voltage can be expressed as VDS=VDG + VGS. With this substitution, the Shichman-Hodges model provides an approximate form for function f(VGS,VDG):
Where:
Kp is a technology related constant associated with the transistor,
W/L is the width to length ratio of the transistor,
VGS is the gate-source voltage, Vth is the threshold voltage, VDS is the
drain-source voltage
λ is the channel length modulation constant
Output resistance
Because of channel-length modulation, the mirror has a finite output resistance given by the ro of the output transistor, namely:
Where:
λ = channel-length modulation parameter
VDS = drain-to-source bias.
Compliance voltage
To keep the output transistor resistance high, VDG = 0 V. That means the lowest output voltage that results in correct mirror behavior, the compliance voltage, is VOUT = VCV = VGS for the output transistor at the output current level with VDG = 0 V, or using the inverse of the f- function, f-1:
For the Shichman-Hodges model, f-1 is approximately a square-root function.
Figure 11.8 shows a mirror where the simple wire connecting the collector of Q1 to its base is replaced by an emitter follower buffer. This improvement to the simple current mirror is referred to as an emitter follower augmented mirror. The current gain (ßQ3) of the emitter follower buffer stage (Q3) greatly reduces the gain error caused by the finite base currents of Q1 and Q2.
Figure 11.8 Buffered Feedback current mirror.
One thing to note that is different in this mirror configuration vs. the simple two transistor mirror is that the Collector-Base voltage, VCB, of Q1 is no longer zero. It is equal to the VBE of Q3. Given the effect of the finite output resistance (Early effect ) the output current IOUT in Q2 will most closely match IIN when the collector voltage of Q2 is the same as that of Q1 which is 2XVBE above the common voltage. Also note that when driven by a resistor, like R1, IIN will now be (V1-VBE1-VBE2)/R1.
Another consequence of adding the emitter follower buffer is, in general, a loss in the frequency response of the mirror. Transistor Q3 is potentially operating at a very small current of 2IB. If there were to be a significant capacitance to ground at the base connection common to Q1 and Q2 the current available to discharge this current will also be small equal to 2IB. But the current available to charge this node is potentially equal to ßQ3IIN which is very much larger than 2IB. This asymmetry in the charging vs. discharging current available for this node in the current mirror can lead to very undesirable response to fast changes to IIN.
A Wilson current mirror or Wilson current source, named after George Wilson, is an improved mirror circuit configuration designed to provide a more constant current source or sink. It provides a much more accurate input to output current gain. The structure is shown in figure 11.9.
Figure 11.9 The Wilson Current Mirror
We will be making the following two assumptions. First, all transistors have the same current gain ß. Second, Q1 and Q2are matched, so their collector currents are equal. Therefore, IC1 = IC2 (= IC) and IB1 = IB2 (= IB) .
The base current of Q3 is given by,
The emitter of Q3 current by,
Looking at figure 11.9, it can be seen that IE3 = IC2 + IB1 + IB2 Substituting for IC2, IB1 and IB2, IE3 = IC + 2IB
so,
Substituting for IE3
rearranging,
The current through R1 is given by, IR1 = IC1 + IB3
But, IC1 = IC2 = IC
Substituting for IC and since
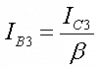 we get,
we get,
Therefore,
And finally,
From the above equation we can see that if
And the output current (assuming the base-emitter voltage of all transistors to be 0.7 V) is calculated as,
Note that the output current is equal to the input current IR1 which in turn is dependent on V1 and R1. If V1 is not stable, the output current will not be stable. Thus the circuit does not act as a regulated constant current source.
In order for it to work as a constant current source, R1 must be replaced with a constant current source.
Advantages over other configurations
This circuit has the advantage of virtually eliminating the base current mismatch of the conventional BJT current mirror thereby ensuring that the output current IC3 is almost equal to the reference or input current IR1. It also has a very high output impedance due to the negative feedback through Q1 back to the base of Q3.
Adding a fourth transistor to the simple Wilson current mirror in figure 11.10, we have the modified or improved Wilson mirror. The improved input to output current accuracy is accomplished by equalizing the collector voltages of Q1 and Q2 at 1 VBE. This leaves the finite ß and voltage differences of each of Q1 and Q2 as the remaining unbalancing influences in the mirror.
Figure 11.10 The improved Wilson Current Mirror
A Widlar current source is a modification of the basic two-transistor current mirror that incorporates an emitter degeneration resistor for only the output transistor, enabling the current source to generate low currents using only moderate resistor values. This circuit is named for its inventor, Robert Widlar, and was patented in 1967.
The Widlar circuit may be used with bipolar transistors or MOS transistors. An example application is in the now famous uA741 operational amplifier, and Widlar used the circuit in many of his designs.
Figure 11.11 A version of the Widlar current source using bipolar transistors.
Figure 11.11 is an example Widlar current source using bipolar transistors, where the emitter resistor R2 is connected in series with the emitter of output transistor Q2, and has the effect of reducing the current in Q2 relative to Q1. The key to this circuit is that the voltage drop across the resistor R2 subtracts from the base-emitter voltage of transistor Q2, thereby reducing the collector current compared to transistor Q1. A simulation plot showing this reduction in IC2 is presented in figure 11.12.
Figure 11.12 Plot of the collector current of Q1 and Q2 R1 = 15KΩ, R2 = 300
This observation is expressed by using KVL around the base emitter loop of the circuit in Figure 11.11 as:
Where ß2 is the beta of the output transistor, which may not be the same as that of the input transistor, in part because the currents in the two transistors are very different. The variable IB2 is the base current of the output transistor, VBE refers to base-emitter voltage. If we neglect the effect of finite ß and use the VBE equation we can obtain a useful formula for the output current:
where VT is the thermal voltage, IIN = IC1 and IOUT = IC2.
Suppose we want to create a 100uA output current from a 300uA input current as in the simulation plot of figure 11.12. VT is 26mV times ln(3) is 28.5mV. 28.5mV divided by 100uA is 285 ohms. This equation makes the approximation that the currents are both much larger than the saturation currents IS1, IS2, an approximation valid except for very low current levels. In the following the distinction between the two scale currents is dropped, although the difference can be important, for example, if the two transistors are designed with different emitter areas.
Figure 11.13 Small-signal circuit for finding output resistance of the Widlar source shown in figure 11.11.
A test current I/x is applied at the output, and the output resistance is then RO = Vx / Ix.
An important property of a current source is its small signal incremental output impedance, which should ideally be infinite. The emitter degeneration resistance introduces local current feedback for transistor Q2. Any increase in the current in Q2 increases the voltage drop across R2, reducing the VBE for Q2, thereby countering the increase in current. This feedback means the output impedance of the circuit is increased, because the feedback involving R2 forces use of a larger voltage to drive a given current.
Output resistance is found using a small-signal model for the circuit, shown in Figure 11.13. The transistor Q1 is replaced by its small-signal emitter resistance rE because it is diode connected. In a diode-connected transistor the collector is short-circuited to the base, so the transistor collector-base junction has no time-varying voltage across it. As a result, the transistor behaves like the base-emitter diode, which at low frequencies has a small-signal circuit that is simply the resistor rE = VT / IE, with IE the DC Q-point emitter current. The transistor Q2 is replaced with its hybrid-pi model. A test current Ix is attached at the output.
Using the figure, the output resistance is determined using Kirchhoff's laws. Using Kirchhoff's voltage law from the ground on the left to the ground connection of R2:
Rearranging:
Using Kirchhoff's voltage law from the ground connection of R2 to the ground of the test current:
or, substituting for Ib:
Eq. 4
According to Eq. 4, the output resistance of the Widlar current source is increased over that of the output transistor itself (which is rO) so long as R2 is large enough compared to the rp of the output transistor. (Large resistances R2 make the factor multiplying rO approach the value (ß +1).) The output transistor carries a low current, making rp large, and increase in R2 tends to reduce this current further, causing a correlated increase in rp. Therefore, a goal of R2 » rp can be unrealistic, and further discussion is provided below. The resistance R1 / rE usually is small because the emitter resistance rE usually is only a few ohms.
ADALM1000 Lab Activity 6, BJT Current Mirror
ADALM1000 Lab Activity 6M, MOS Current Mirror
ADALM2000 Lab Activity 6, BJT Current Mirror
ADALM2000 Lab Activity 6M, MOS Current Mirror
When designing a circuit it is important to take into account the wide variation in certain device values from one to another. A central objective of the designer is to desensitize the circuit to these variations to produce a circuit which meets the specifications across all possible conditions. One aspect of design which is common to nearly all circuits is the establishment of stable bias or operating point levels. This seemingly minor portion of a design can provide the most challenging and interesting circuit problems. Many bias generators are centered around the generation of currents to operate the core of the circuit. Current generated from simple resistors and diodes or diode connected transistors connected across the power supply will vary approximately proportional to the variation of the supply voltage. This variation in the resulting bias current is frequently undesirable.
This is to introduce another kind of current mirror, actually a stabilized current source, which has an output which had been desensitized to variation in input current. To understand this configuration, it is helpful to examine the behavior of a zero gain amplifier. A NMOS version is shown in figure 11.14 but PMOS, NPN or PNP transistors will just as well function in this configuration
Figure 11.14 NMOS Zero Gain Amplifier
Remembering back to the previous explanation of the common emitter/source amplifier (figure 11.14(a)), the gain is a function of the drain (or collector) current and the load resistor. For a given drain current, if the drain resistor RL is set equal to rs then the gain A will be minus 1.
Alternatively. if the gate is held fixed at the same DC bias level which produces an identical drain current as in (a) and an input signal is applied to the top of load resistor RL (figure 11.14(b)), then the gain will be plus 1. That is if the drain/source output impedance of the transistor is neglected. If we now connect the gate to the top of resistor RL as in figure 11.14©, the net gain superimposing both paths will be 1 - 1 = 0.
In figure 11.15 we have an NPN transistor biased into conduction with a collector voltage VC which is less than the base voltage VBE by the thermal voltage VT= kT/q, (equal to Ic times RL) and is essentially constant with input voltage changes applied from VIN. The voltages seen at VBE and VC are plotted vs. the applied voltage at VIN in figure 11.14. As we can see while VBE continues to rise, VC remains much more constant and actually decreases above a certain level of VIN.
Figure 11.15 NPN Zero Gain Amplifier
Figure 11.16 Plot of VBE and VC vs VIN for R1 = 10KΩ and RL=75Ω
A zero gain amplifier made using an enhancement mode NMOS 2N7000 transistor was simulated where the small signal AC gain and phase was calculated as the drain current was swept. As can be seen in figure 11.17 there is a sharp null or dip in the gain curve at around 345uA. This also occurs at the point where the phase makes a sharp transition from 0 degrees to 180 degrees.
Figure 11.17 Small signal gain/phase plot of zero gain amplifier vs. ID
ADALM1000 Lab Activity 7, BJT Zero Gain Amplifier
ADALM1000 Lab Activity 7m, NMOS Zero Gain Amplifier
ADALM2000 Lab Activity 7, BJT Zero Gain Amplifier
ADALM2000 Lab Activity 7m, NMOS Zero Gain Amplifier
Now that we understand the concept of the zero gain amplifier, the objective is to investigate its use to produce an output current which is stabilized (less sensitive) to variations of the input current level. This current source configuration, figure 11.17, is also sometimes called a Peaking Current Source or gm-compensated mirror. Because the collector voltage VC of transistor Q1 is now more constant with changes in the input supply voltage as represented by VIN, it can be used as the base voltage of Q2 to produce a much more constant collector current in transistor Q2.
Figure 11.18 Stabilized (Peaking) current source (gm-compensated mirror)
Figure 11.19 Plot of the collector current of Q1 and Q2 R1 = R2 = 10KΩ, RL = 75Ω
Figure 11.20 PTAT current plot of Peaking Current Source
Figure 11.21 A combination of the Widlar mirror and peaking current source provides further improvement in the regulation of a variable input current.
Figure 11.22 Simulation of circuit in figures 11.18 and 11.21 with R1 = 20KΩ, RL= 250Ω and R2= 1.2KΩ
Figure 11.23 cascade of NPN and PNP peaking current sources
ADALM1000 Lab Activity 8, BJT Stabilized current source
ADALM1000 Lab Activity 8m, NMOS Stabilized current source
ADALM2000 Lab Activity 8, BJT Stabilized current source
ADALM2000 Lab Activity 8m, MOS Stabilized current source
Return to Previous Chapter
Go to Next Chapter
Return to Table of Contents